Rappels sur les nombres binaires

Sommaire

Le système binaire (de base deux) est fondé sur deux chiffres, le plus souvent 0 ou 1. À l’opposé, le système décimal (de base dix) est fondé sur dix chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8 ou 9).
Les ordinateurs ne savent pas compter au-delà de 1.
Un tel nombre est dit binaire, car il ne comporte que deux chiffres, alors que nos nombres habituels en comporte dix, ils sont décimaux.

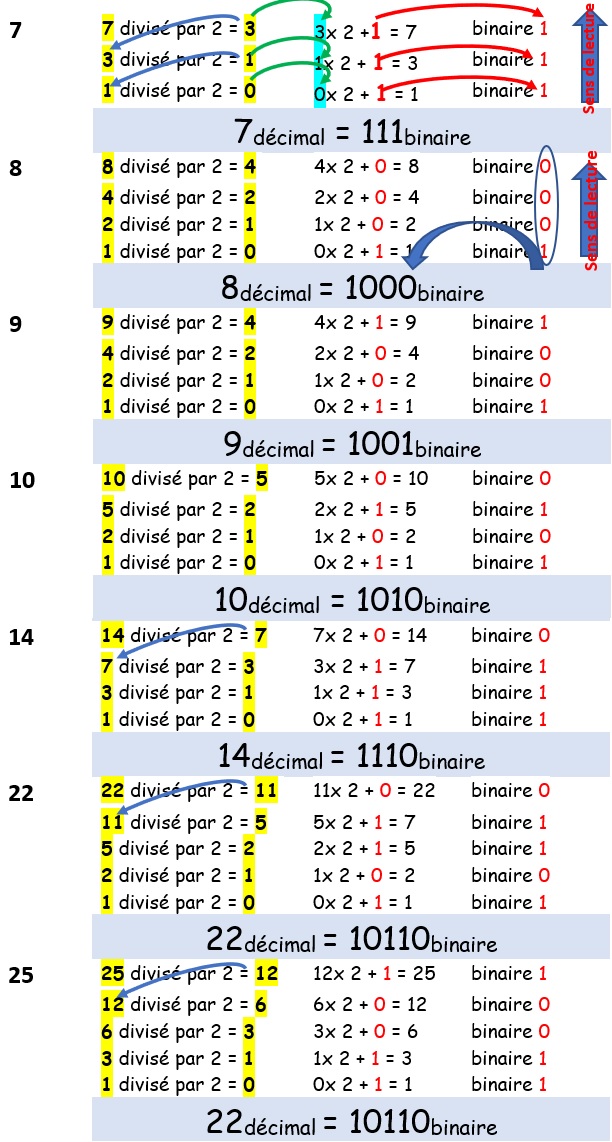
La conversion de la partie entière d’un nombre décimal en nombre binaire consiste en des divisions successives par 2 jusqu’à ce qu’un 0 soit obtenu comme quotient avec un reste de 1.
La méthode débute par la division du nombre par 2, le reste est reporté comme le bit du poids le plus faible (bit de rang 0).
Le quotient de cette division est, lui aussi, divisé par 2.

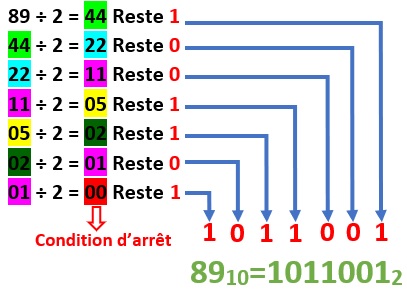
La division de 89 par 2 donne un quotient de 44 avec un reste de 1 qui sera le bit du poids le plus faible.
Le quotient de cette première division, 44, est ensuite divisé par 2 pour donner un quotient de 22 avec un reste de 0, c’est le bit 1 (deuxième bit à gauche).
La division de 22 par 2 donne 11 avec un reste de 0 qui sera le bit 2.
La division de 11 par 2 donne 05 avec un reste de 1 qui sera le bit 3.
La division de 05 par 2 donne 02 avec un reste de 1 qui sera le bit 4 et ainsi de suite.
Vous remarquez que l’avant-dernière division (2/2) donne un quotient de 1, lequel divisé par 2 donne 0 comme quotient et 1 comme reste. La conversion est alors terminée.

Références:

PHP