Rotation et Symétrie
Rotation et Symétrie
-
Présentation
- Un test de QI peut également inclure des questions sur l´identification de formes et de figures.
- Une de ces techniques est connue sous le nom de « rotation et la symétrie ».
- La difficulté réside dans la représentation de ce cube une fois plié. Cet exercice se présente sous la forme de questions à choix multiples. Celles-ci vous amènent à effectuer des exercices de rotation mentale de figures et reposent donc sur votre intelligence spatiale.
- La rotation et la symétrie sont les principales transformations utilisées dans les tests graphiques. Ainsi, nous vous proposons une fiche de cours ainsi que plusieurs tests afin de vous familiariser avec ce type d’exercices.
-
Rotation
-
Définition
- La rotation est le mouvement d’un corps autour d’un point ou d’un axe. Usuellement, le terme « rotation » est utilisé pour les mouvements circulaires, que ce soit pour un moteur ou pour qualifier le mouvement d’un astre sur lui-même.
-
Sens de rotation
- Le sens de rotation est le sens dans lequel a lieu une rotation. Il en existe deux, qui sont nommés différemment selon les contextes. Le sens de rotation est généralement représenté par une flèche en forme d’arc de cercle.
- La rotation qui consiste à faire tourner autour d’un point.
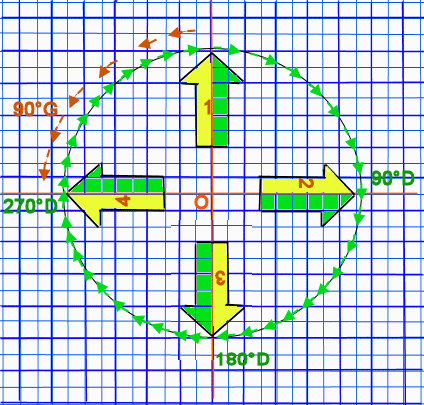
- La rotation est le déplacement d’une figure par rapport à un centre de rotation ( ici, O) et selon un angle de rotation et un sens de rotation.
- Nous nous limiterons aux rotations de 90°, 180°, 270°, 360° ( nous retournons alors à l’origine de la figure en ayant fait un tour complet).
- C’est un mouvement circulaire selon un cercle ou un arc de cercle.
- Pour passer de la position 1 à la position 2, notre figure a effectué une rotation de 90°( 1/4 de tour), ‘vers la droite’ (dans le sens des aiguilles d’une montre) par rapport au point O, le centre de rotation.(90°D).
- Pour passer de la position 1 à la position 3, la rotation est de 180° ‘vers la Droite’, mais on obtiendrait la même position ‘vers la gauche’ (dans le sens contraire des aiguilles d’une montre)(car nous avons effectué 1/2 tour.
- Pour passer de la position 1 à la position 4, la rotation est de 270° ‘vers la Droite'( 3/4 de tour) , mais on obtiendrait la même position par une rotation de 90° ‘vers la gauche'( en rouge).
- Dans tous les cas, lors d’une rotation, la figure garde sa forme, ses dimensions mais change d’orientation.
-
Sens horaire
- Lorsque la figure pivote (ou se déplace) dans le sens horaire, la rotation se fait dans le :
- sens des aiguilles d’une montre
- sens anti-trigonométrique
- sens négatif
- sens indirect
-
Sens anti-horaire
- Lorsque la figure pivote (ou se déplace) dans le sens anti-horaire, la rotation se fait dans le :
- sens contraire des aiguilles d’une montre
- sens inverse des aiguilles d’une montre
- sens trigonométrique
- sens positif
- sens direct
-
Angle de rotation
- En mathématiques , l’ angle de rotation est une mesure de la quantité, l’ angle , par lequel une figure est tournée dans le sens inverse des aiguilles d’une montre autour d’un point fixe.
- Une rotation dans le sens des aiguilles d’une montre est considérée comme une rotation négative, de sorte qu’une rotation de 310 ° (sens inverse des aiguilles d’une montre) peut également être appelée rotation de -50 ° ( 310 ° + 50 ° = 360 ° , rotation complète).
- Une rotation dans le sens contraire des aiguilles d’une montre de plus d’un tour complet est normalement mesurée modulo 360 °, ce qui signifie que 360 ° est soustrait autant de fois que possible pour laisser une mesure non négative inférieure à 360 °.
-
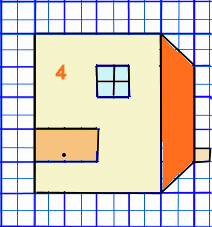
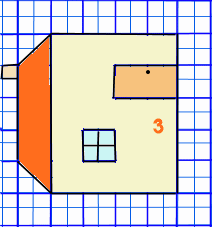
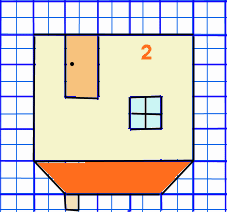
Exemple de rotation
- Soit l’image de départ suivant
- Effectuer une rotation de 90° de tour dans le sens contraire des aiguilles d’une montre.==> ‘vers la gauche‘.
- Pour obtenir l’image 2 en partant de la 4, j’effectue une rotation de 90° ‘vers la droite’.
- Pour revenir à l’image 4 en partant de la position 2 , j’effectue une rotation de 270° dans le sens des aiguilles d’une montre.
-
Symétrie
- Un système est symétrique quand on peut permuter ses éléments en laissant sa forme inchangée.
- Une symétrie géométrique est une transformation géométrique involutive qui conserve le parallélisme. Parmi les symétries courantes, on peut citer la réflexion et la symétrie centrale.

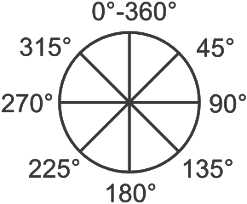

Faire une rotation est de 90° de tour dans le sens des aiguilles d’une montre.==> ‘vers la droite‘.