Algorithme: la récursivité

.hovertable {
font-family: verdana,arial,sans-serif;
font-size:11px;

margin: -2px;
width: 100%;
overflow: hidden;
background: #FFF;
color: #024457;
border:2px solid #167F92;
border-radius: 10px;
border-collapse: separate;
}
.hovertable th {
background-color:#c3dde0;
border-width: 1px;
color:#024457;
padding: 8px;
border-: solid;
border-color: #a9c6c9;
}
.hovertable tr {
border: 1px solid #D9E4E6;

&:nth-child(odd) { // highlight the odd rows with a color
background-color: #EAF3F3;
}
.hovertable td {
border-width: 1px;
padding: 8px;
border-: solid;
border-color: #a9c6c9;
}

summary {
cursor: pointer;
font-size: 16px;
font-weight: bold;
text-decoration-line: overline underline line-through;
}

.coin {
background-color:#E4EFFF;
border:1px solid #9FC6FF;
padding:5px;
/*arrondir les coins en haut à gauche et en bas à droite*/
-moz-border-radius:10px;
-webkit-border-radius:10px;
border-radius:10px;
font-family: ‘Trebuchet MS’, Verdana, sans-serif;
}

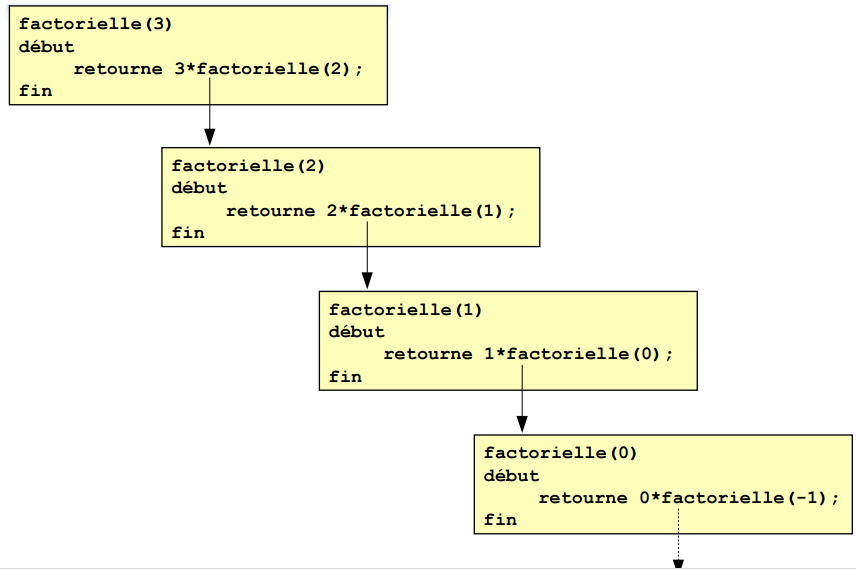
Algorithme: la récursivité

// Définitions On appelle récursive toute fonction ou procédure qui s’appelle elle même. Exemple : la factorielle, [latex]n! = 1 x 2 x … x n[/latex] donc [latex]n! = n x (n-1)! [/latex] L’appel récursif est traité comme n’importe quel appel de fonction. La récursivité est un concept général qui peut être illustré dans (quasiment) tous les langages de programmation, et qui peut être utile dans de nombreuses situations. Les fonctions récursives sont des fonctions qui s’appellent elles-mêmes. Elles doivent donc résoudre des problèmes qui “s’appellent eux-mêmes”. Dans certains d’entre eux, la solution du problème général demande la résolution de plusieurs sous-problèmes particuliers, qui sont semblables au premier problème. Par exemple, on peut dire que pour résoudre le problème « combien vaut la factorielle de 4 ? » , il faut résoudre le problème « combien vaut la factorielle de 3 ? » . La récursivité est une méthode algorithmique qui consiste à appeler un sous programme dans son propre corps. Un sous-programme récursif est un module qui fait appelle à lui-même. A chaque appel, il y a mémorisation d’une valeur différente d’un paramètre formel. Un programme récursif doit : Avoir au moins un point d’arrêt (une condition de sortie) pour ne pas être dans une boucle infinie. Avoir un ou plusieurs traitements représentés par des appels récursifs. Présentation et utilisations Puisqu’une fonction récursive s’appelle elle-même, il est impératif qu’on prévoit une condition d’arrêt à la récursion, sinon le programme ne s’arrête jamais! On doit toujours tester en premier la condition d’arrêt, et ensuite, si la condition n’est pas vérifiée, lancer un appel récursif. Applications On se propose de calculer et d’afficher la valeur de x à la puissance n. x et n sont respectivement un réel et un entier donnés. Questions : a) Analyser le problème en utilisant un module récursif, b) Donner les algorithmes correspondants, c) Traduire l’ensemble en un programme Pascal. a) Analyse du programme principal Résultat = Ecrire (x, ” à la puissance “, n, ” = “, Fn Puissance (x, n)) X = donnée (“Donner un réel :”) N= donnée (“Donner un entier :”) Fin PP Contenu du chapitre :Algorithme: la récursivité 1.Définitions et utilisations 2.QCM 3.Exercices 4.Examens corrigés Sommaire du cours Algorithme

(adsbygoogle = window.adsbygoogle || []).push({});