Algorithme: la récursivité
Algorithme: la récursivité

-
Définitions
- On appelle récursive toute fonction ou procédure qui s’appelle elle même.
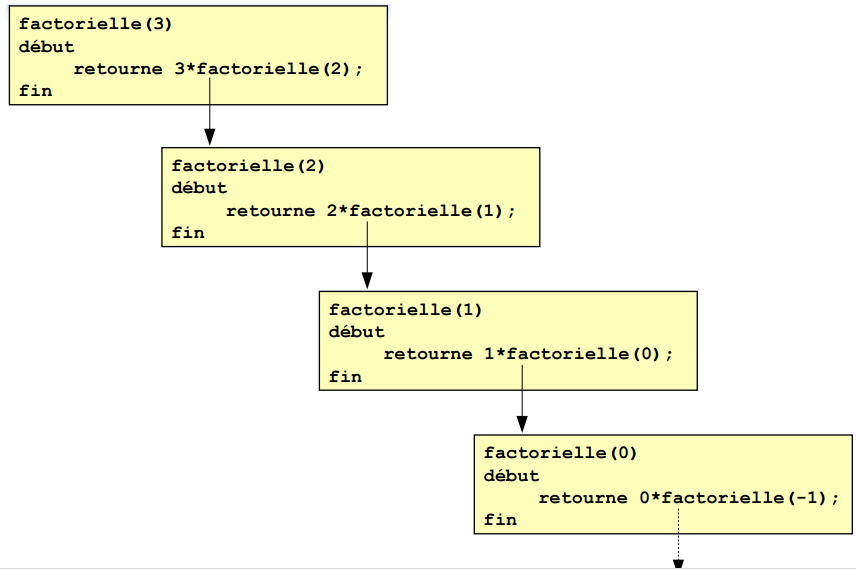
- Exemple : la factorielle, [latex]n! = 1 x 2 x … x n[/latex] donc [latex]n! = n x (n-1)! [/latex]
- L’appel récursif est traité comme n’importe quel appel de fonction.
- La récursivité est un concept général qui peut être illustré dans (quasiment) tous les langages de programmation, et qui peut être utile dans de nombreuses situations.
- Les fonctions récursives sont des fonctions qui s’appellent elles-mêmes.
- Elles doivent donc résoudre des problèmes qui « s’appellent eux-mêmes ».
- Dans certains d’entre eux, la solution du problème général demande la résolution de plusieurs sous-problèmes particuliers, qui sont semblables au premier problème. Par exemple, on peut dire que pour résoudre le problème « combien vaut la factorielle de 4 ? » , il faut résoudre le problème « combien vaut la factorielle de 3 ? » .
- La récursivité est une méthode algorithmique qui consiste à appeler un sous programme dans son propre corps.
- Un sous-programme récursif est un module qui fait appelle à lui-même. A chaque appel, il y a mémorisation d’une valeur différente d’un paramètre formel.
- Un programme récursif doit :
- Avoir au moins un point d’arrêt (une condition de sortie) pour ne pas être dans une boucle infinie.
- Avoir un ou plusieurs traitements représentés par des appels récursifs.
-
Présentation et utilisations
- Puisqu’une fonction récursive s’appelle elle-même, il est impératif qu’on prévoit une condition d’arrêt à la récursion, sinon le programme ne s’arrête jamais!
- On doit toujours tester en premier la condition d’arrêt, et ensuite, si la condition n’est pas vérifiée, lancer un appel récursif.
-
Applications
- On se propose de calculer et d’afficher la valeur de x à la puissance n. x et n sont respectivement un réel et un entier donnés.

Questions :
-
a) Analyser le problème en utilisant un module récursif,
b) Donner les algorithmes correspondants,
c) Traduire l’ensemble en un programme Pascal.
a) Analyse du programme principal
-
Résultat = Ecrire (x, » à la puissance « , n, » = « , Fn Puissance (x, n))
-
X = donnée (« Donner un réel : »)
N= donnée (« Donner un entier : »)
Fin PP
